GeoDataFrame使操作GIS資料分析時更有彈性
我們可以很快對GIS的屬性資料的分析與過濾

當然，也包括一些幾何空間的運算

大綱:

• 坐標轉換
• 幾何操作
• 空間運算子

坐標轉換

坐標轉換幾乎是GIS第一門課，有關坐標系統及坐標轉換，可以參考去年的文章[Day10] 坐標系統及WebGIS常用的坐標轉換有大致的整理及說明。

Geopandas依賴pyrpoj，proj是坐標轉換非常方便的工具，
也因此，在Geopandas坐標轉換變得很簡單(但要記得轉對及搞懂啊!)
我們以昨天的圖書館資料為例，昨天有提到，它是epsg4326(WGS84)，試著轉成epsg3826(TWD97)

為什麼要轉呢? 在同一坐標系統的資料才能一起操作

有關圖書館資料，請參考Day03 從Pandas到Geopandas的幾種方法

import geopandas as gpd
gdf_Lib=gpd.read_file('output/Library.shp',encoding='utf-8')
gdf_Lib.crs = {'init' :'epsg:4326'} # 避免資料沒設，這邊再重新給一次
gdf_Lib=gdf_Lib.to_crs(epsg=3826)
gdf_Lib

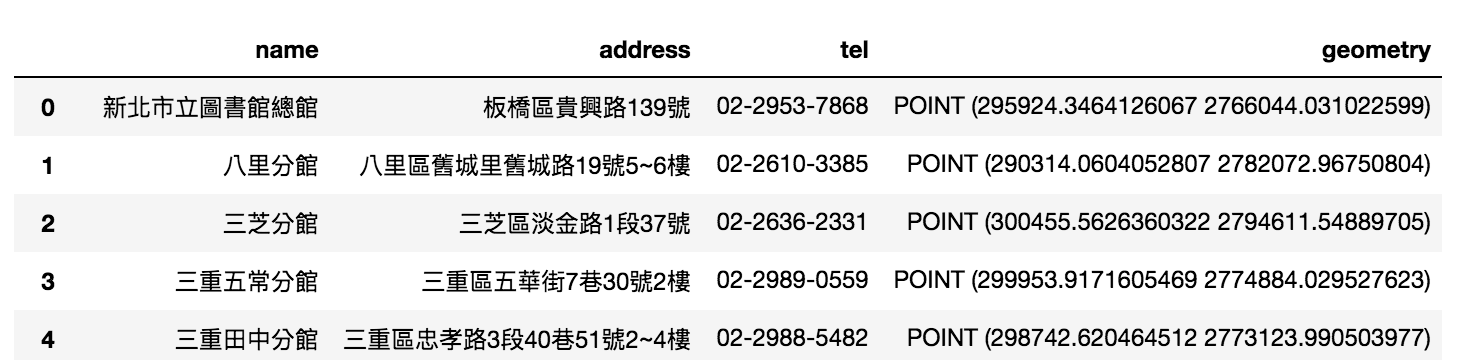
可以看到坐標系統已經成功轉換為TWD97(4326-->3826)

幾何操作

接下來來進行基本的幾何運算，
Geopandas的幾何操作主要是來自shaply套件，以下來試看看在GIS軟體常用的功能

buffer

buffer在GIS中常用來分析點線面的影響範圍，
這邊採用上面圖書館的資料
採用buffer這個方法，參數為環域距離

由於坐標系統已經轉為TWD97，因此距離的設定的單位為公尺

而為了做比較，我們只取資料的第一筆做buffer，並把原始的點也放上去。

base=gdf_Lib.head(1).buffer(100).plot()

gdf_Lib.head(1).plot(ax=base, marker='o', color='red', markersize=30);

area

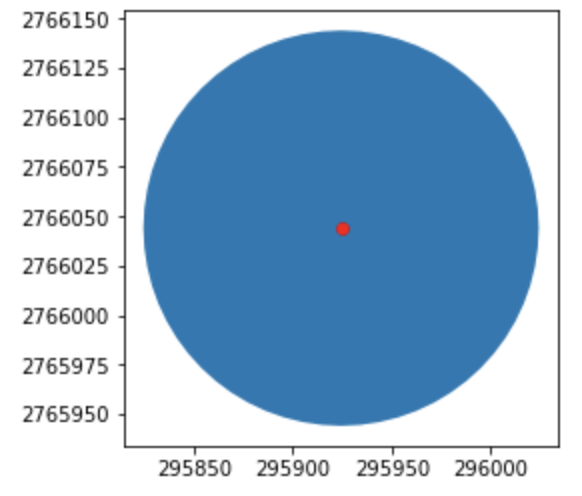
area是GeoDataFrame中，提供每一筆幾何資料的面積

buffer=gdf_Lib.head(1).buffer(100)
area=buffer.area
print(area[0])

### # 0 31365.4849055

envelope

envelope是整個GeoDataFrame中，每一筆資料包覆的長方形範圍，它是一個四角坐標

envelope=buffer.envelope
print(envelope)


# 0    POLYGON ((295824.3464126067 2765944.031022599,...

convex_hull

convex hull與envelope類似但不一樣，它是包住每一個資料的凸殼多邊形

convexhull=buffer.convex_hull
print(convexhull)

### 0    POLYGON ((295924.3464126067 2765944.031022599,...

可以把圖畫出來，看看convex hull與envelope，
我們連同原本的形狀一起套疊(原本的形狀是由點buffer成面)

base=envelope.plot()
convexhull.plot(ax=base,color='brown')
gdf_Lib.head(1).plot(ax=base,  color='red');

可以發現convex hull與envelope的差異，並且convex hull與buffer的結果一樣(因為包住圓的convex hull 也是圓..不好意思這個例子好像舉的不太好)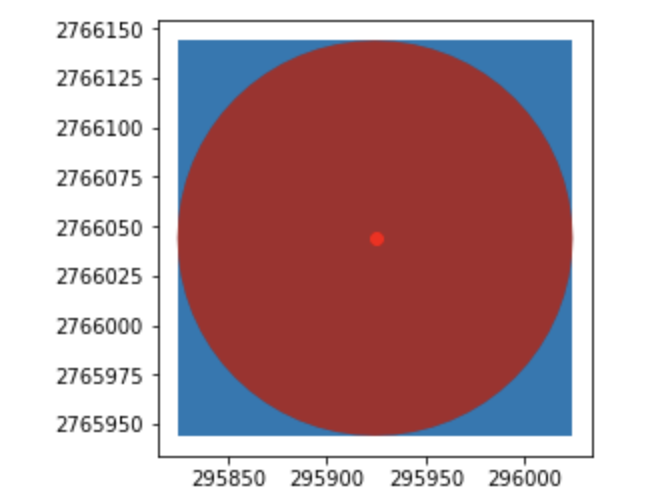

幾何轉換

Geodataframe可以進行幾何的投影轉換，
支援仿射轉換(Affine Transform)，包含了兩個平移、兩個尺度、一個剪力以及一個旋轉

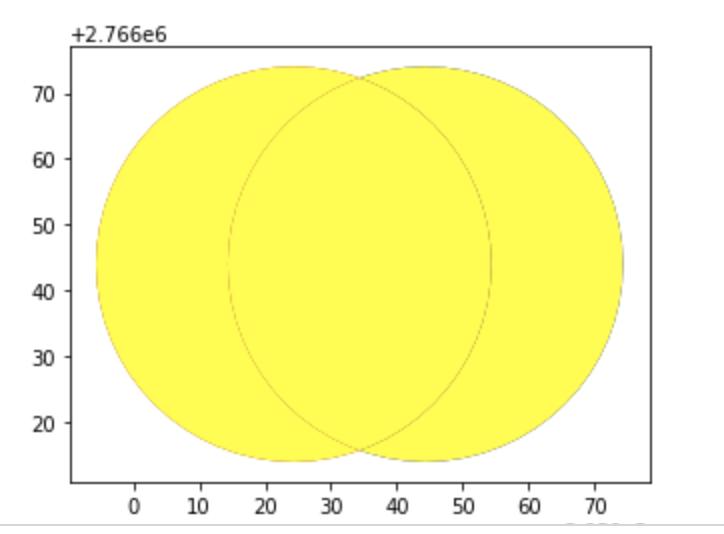
這邊只舉尺度轉換的例子，分別在x方向10倍及y方向5倍的投影，並與原本的buffer展圖比較。

base=buffer.scale(10,5).plot(color='yellow')
buffer.plot(ax=base,color='brown')

其餘的一些操作在Shapely的官方文件有滿多說明的，特別是對幾何資料的一些檢查，建議有需要時瀏覽一遍Shapely的參考文件
The Shapely User Manual — Shapely 1.2 and 1.3 documentation

空間運算子

前半部說明的主要為資料內部的計算，在此空間運算子是屬於資料與資料之間的運算與分析

常見的GIS運算包含了幾項運算子，如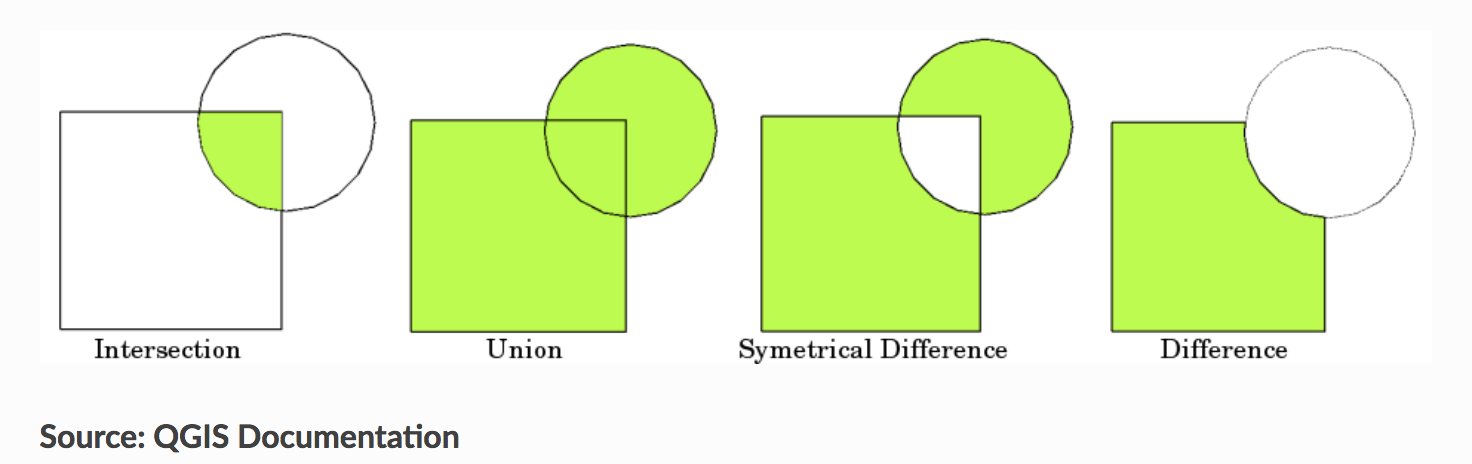
[取自Geopandas/QGIS]

為了方便說明空間運算子的產出，
我們把前面buffer的成果做一些處理做空間運算子的測試，

其中，p1是把buffer成果做一些平移，p2則是原本buffer的結果

p1=gpd.read_file('output/Library.shp',encoding='utf-8').head(1)
p1.crs = {'init' :'epsg:4326'} # 避免資料沒設，這邊再重新給一次
p1=p1.to_crs(epsg=3826)
p1['geometry']=p1.buffer(30).translate(xoff=20.0, yoff=0.0)

p2=gpd.read_file('output/Library.shp',encoding='utf-8').head(1)
p2.crs = {'init' :'epsg:4326'} # 避免資料沒設，這邊再重新給一次
p2=p2.to_crs(epsg=3826)
p2['geometry']=p2.buffer(30)

intersection

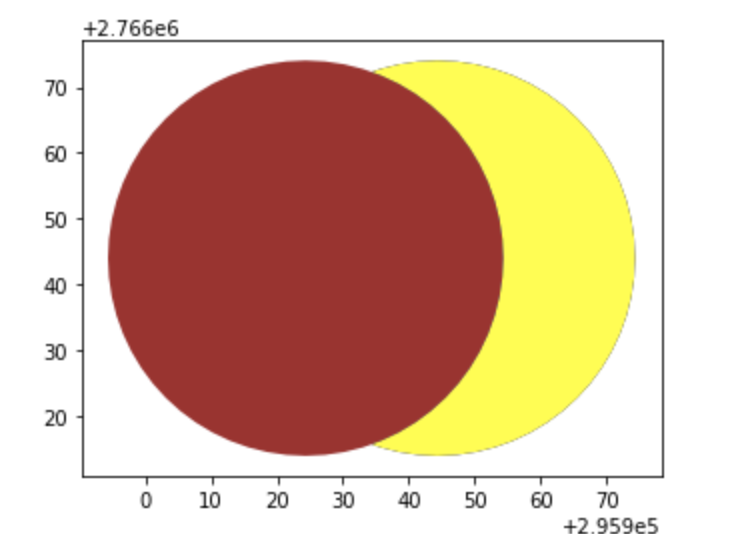
第一個運算子是intersection，算出的是兩個圖形的交集，
我們分別使用不同的顏色給p1與p2，並把交集的部分給定黃色

intersection = gpd.overlay(p1,p2,  how='intersection')
base=p1.plot(color='blue')
p2.plot(ax=base,color='brown')
intersection.plot(ax=base,color='yellow')

union

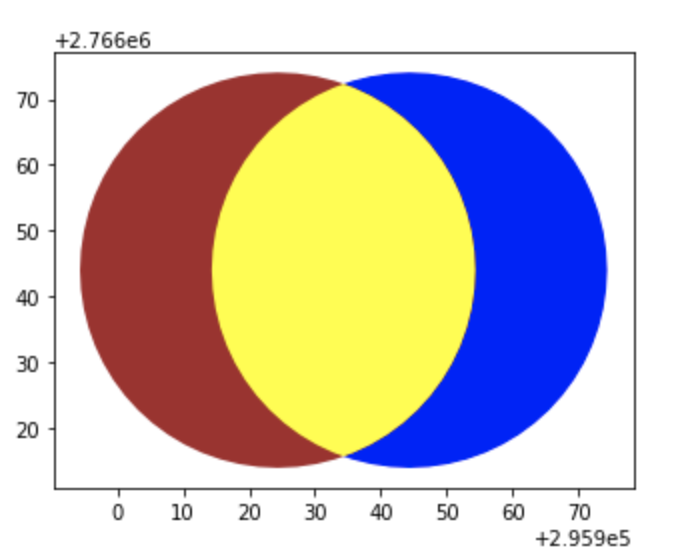
第二個是union聯集，一樣給予上色，黃色的部分，就是聯集的部分

union = gpd.overlay(p1,p2,  how='union')
base=p1.plot(color='blue')
p2.plot(ax=base,color='brown')
union.plot(ax=base,color='yellow')

difference

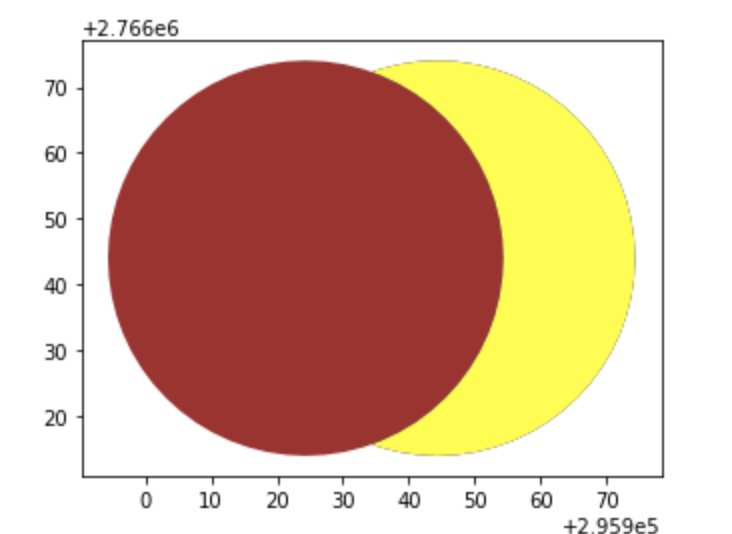
difference會算出兩個幾何的差異，一樣以黃色表示

difference = gpd.overlay(p1,p2,  how='difference')
base=p1.plot(color='blue')
p2.plot(ax=base,color='brown')
difference.plot(ax=base,color='yellow')

以上就簡單測試一些幾何運算子，未來幾天有機會會在應用到這些方法

今天的相關測試可以參考GitHub

本文同步發表於個人部落格